If you have worked in SAP Material Management (MM), you likely have dealt with the rounding of material quantities. The issues come in various forms - but often occur in conversions between Unit of Measure (UOM) in orders, inventory levels or material transfers.
For example, an order or transfer can be for cases (3 cases of soap) or single units (3 bottles of soap) or both (2 cases and 3 bottles). How do you reflect this in SAP? As is almost always the case with SAP, it depends … on how your SAP system is configured.
The Problem
First, a bit of context. Our company, CNBS Software, builds solutions (mobile, eCommerce and Fiori apps) that integrate with existing SAP systems. This means we must deal with whatever SAP configuration we are given. In one recent scenario, we worked on a mobile application for a customer that sells products in bulk, and whose SAP system was configured to use case (CS) as the base unit of measure. As often happens in real life, there were exceptions and some products could still be sold (or sometimes given away) as single units. To manage this, each (EA) was configured as an alternative UOM. This customer also required that products couldn’t be added to orders unless there was enough inventory in the seller’s assigned storage location (SLOC).
Having the bigger measurement (case) as the default UOM generated some interesting problems, especially when paired with the requirement only to sell inventory they actually had. Let’s take a look at an example where a product had 6 single units per case (like a six-pack) and follow some scenarios that needed to be handled properly.
Since the base UOM was configured as case in their SAP system, all inventory and material movements were expressed in CS. When the products were sold in single units, the result was fractions: an inventory of 3.167 meant you actually have 3 CS and 1 EA.
If we look at the math in case of a six-pack, a single unit is 1/6 of a case or 0.167 CS (when rounded to 3 decimal places). Every time 1 single unit is sold, 1/6 or 0.167 CS is deducted from the inventory. Assuming you start with 1 CS and sell 1 EA at a time, after the first sale you are left with (1.000 CS – 0.167 CS) 0.833 CS. You could sell the remaining 5 EA in one order because SAP will calculate 5 single units as 0.833 CS (5/6 = 0.833). In this case, you would end up with 0 inventory (e.g. you sold 1, then 5). However, if you keep selling single units on separate orders, you will get the following results:
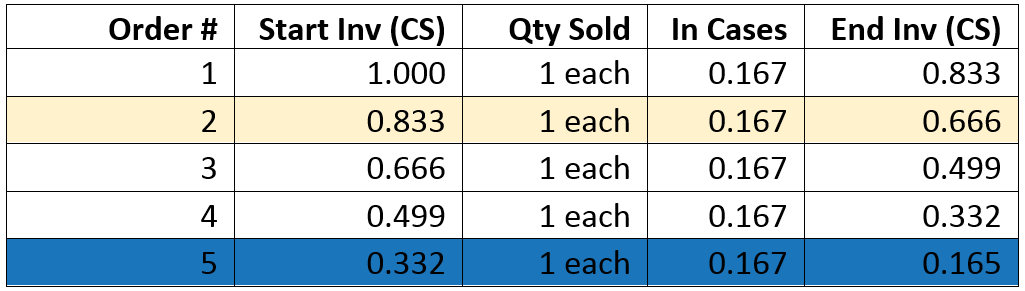
After selling just 2 single units, issues begin to arise. If you want to sell the 4 remaining in one order, SAP needs to deduct 4/6 or 0.667 CS from the inventory, but it only has 0.666 CS and the SAP inventory check will fail (preventing the sale). If you keep selling one at a time, you can still sell only the first 5 EA. Your inventory after the 5th will be 0.165 CS, which is clearly less than the 0.167 need to sell 1 EA. Apart from orders, this also affects transfers from one SLOC to another: a salesperson could sell 2 EA from SLOC A and then try to transfer the remaining 4 to a coworker in SLOC B but SAP will not allow the transfer.
The Solution
There are certainly smart ways of dealing with UOM conversion issues through configuration. But to do so in this case would have required modifying the customer´s SAP system and affecting many of their internal processes. Our team decided on an approach that handled most of the issues in our mobile app (and related ABAP code that our mobile app used to interface with SAP). The solution came in two parts.
Part 1 – Keep it clean and pass the buck
Our approach was inspired by a lesson many parents teach their children: when you stay somewhere, leave the place in the same (or better) condition than you found it. Applying this same idea to transferring between storage locations, we decided to always leave the source SLOC in an ideal state, passing the rounding problems to the target SLOC.
Using our example of a six-pack, let’s first look at what happens when we transfer 1EA from SLOC A to SLOC B without any special handling:
Starting Inventory SLOC A: 1.833 (1CS and 5EA)
Amount to transfer out (1 EA): 0.167 as converted by SAP
Ending Inventory SLOC A: 1.666 (1.833 - 0.167)
We moved 1 EA, so our ending inventory should be 1CS and 4EA (or 1.667 CS as calculated by SAP). Instead we end up with 1.666 CS. If we now place an order (or attempt to transfer) 1 CS and 4EA, SAP will reject it due to insufficient inventory.
To handle this, we adjusted the transfer quantity by a small fraction to make sure the inventory in the source SLOC after the transfer was correct. Here is an example what how that works:
Starting Inventory in SLOC A: 1.833 CS (or 1 CS and 5 EA)
Amount to transfer out: 1 EA
Ending inventory should be: 1CS and 4EA (or 1.667 CS)
Actual transfer amount is calculated as: 1.833CS (start) - 1.667CS (end) = 0.166 CS
Actual ending inventory in SLOC A: 1.667 (1.833 CS start - 0.166 CS transferred)
Actual ending inventory in SLOC B: 2.166 (let’s assume it started with 2.000 CS)
While SLOC A now has a clean balance, you may think “Wait a minute … all you did was push the problem to SLOC B.”
This is true, and where part 2 of the solution comes in to play.
Part 2 – Decimal Dust Adjustments
In this case, the fraction problem must be handled during processing of the sales order. From time to time, we also need to reconcile products quantities in the various SLOCS (e.g. when doing ad-hoc or cycle counts).
Continuing the example from part 1, our SLOC B started with 2.000 CS, and ended with 2.166 CS (since we transferred an adjusted 1EA or 0.166 CS into it). If we now want to sell all our inventory, SAP requires 2.167 CS (2 CS + 0.167 CS) - but shows that our SLOC has only 2.166 CS. We are .001 cases short.
Our solution implemented the logic inside our ABAP order processing code. First, we detected if the required quantity was slightly below what the SLOC had and, if so, dynamically `bumped´ the quantity by the fractional dust amount, so it matched the order´s requirement. Then we processed the sales order normally. This is like doing an on-the-fly material count on that SLOC, which corrects the inventory to the amount SAP needs to process the order. Our logic applied this adjustment only when the discrepancy was below a certain threshold (10-20% of EA) to safeguard against selling an extra unit that the customer didn’t have.
Similar logic was applied during product counting. Our mobile app allows salespeople to count physical inventory on hand and submit any discrepancies (e.g. lost/damaged product). When counting, salespeople enter what they have on hand and the app tells them if it matches what SAP thinks they have (based on the SLOC transaction history). During this check, our mobile app does threshold adjustments to handle `decimal dust´ mismatches (e.g. when a salesperson counts 1 case but SAP lists 0.999 CS). When the salesperson submits the final count, quantities in SAP are adjusted to match what was counted, providing a secondary path to removing fractional discrepancies caused by rounding in CS to EA conversions.
Other Implications
While UOM fractions are fine inside SAP, they can be awkward for the humans who deal with them. For example, most customers will be puzzled when they see an invoice for 3.167 cases.
To make our mobile app easier to use for both the salespeople and their customers, we applied specialized logic to convert SAP’s base UOM fractions into more friendly CS-EA representations in customer-facing outputs like screens, orders, invoices and reports. We also supplied custom input controls everywhere salespeople needed to enter quantities. With these controls they can enter cases and units, which are then converted to fractions of CS when sent to SAP.
Our solution, while specific to this customer, used alternative approaches that may be useful to others dealing with similar situations. It allowed our customer’s field sales team to use a real-time SAP integrated mobile application, avoid the nuances of SAP UOM rounding issues, and do their job and sell. It also kept inventory numbers in line with reality and reduced time spent on manual cleanup of decimal dust - which previously was a regular occurrence.




